3030402-31安裝設定941129
3030402-31更改伺服器及防火牆941129
3030402-31網路線及施工工程941129
3030402-31網路施工費960523
3110101-05治療車830630
3140101-01NAS資料儲存設備951110
3140101-01儲存系統960523
3140101-03個人電腦921225
3140103-03個人電腦940630
3140103-08專業聲音素材921225
3140103-08VIRUSHERLOCK教育版930930
3140103-08PACKETSHOW教育版930930
3140103-08不當網頁過濾教育版SYS930930
3140103-08FRONT PAGE最新版950414
3140103-08OFFICE標準最新授權教育版950414
3140103-08電腦動畫製作軟體960111
3140201-01記憶體921225
3140302-01雷射印表機941129
3140302-01印表機記憶體941129
3140304-06彩色掃描器911125
3140307-01液晶螢幕921225
3140307-01顯示器940630
3140307-01顯示器940630
3140401-01校務行政系統891025
3140401-01校務行政系統900912
3140401-01專業影像圖庫影片系統921225
3140401-01網頁設計軟體921225
3140401-01簡報整合軟體921225
3140401-01校務行政系統921222
3140401-01校務行政資訊系統930506
3140401-01校務行政系統930616
3140401-01影像編輯軟體931129
3140401-01校務行政系統940118
3140401-01安裝設定費931230
3140401-01網路認證系統950414
3140401-01校務行政系統960411
3140401-04網路伺服器921225
3140401-04網路伺服器930211
3140401-04網路伺服器930405
3140401-04網路伺服器930412
3140401-04網路伺服器950414
3140401-04網路伺服器950414
3140405-05伺服器960523
3140403-16交換式集線器941129
3140403-16交換式集線器941129
3140403-18乙太網路交換器960523
3140503-001防火牆930930
3140503-01燒錄器921225
3140503-01積體電路燒錄器941129
4050207-03不斷電系統910820
4050207-03不斷電系統950414
4050207-03機架型UPS960523
4050401-07平板天線12 DBI950414
4050401-07平板天線12 DBI950414
4050401-07平板天線12 DBI950414
4050401-07平板天線12 DBI950414
4050401-15全向型天線12 DBI950414
4050401-15全向型天線12 DBI950414
4050401-15全向型天線12 DBI950414
4050401-15全向型天線12 DBI950414
4070102-02基地台941129
4070102-02高階基地台950414
4070102-02基地台950414
4070102-02基地台950414
4070102-02基地台950414
4070102-02基地台950414
5010102-09A懸掛式白板870630
5010104-01數位相機921225
5010105-01數位攝影機及配備911125
5010105-01數位攝影機921225
5010105-01數位攝影機921225
5010105-01攝影機931129
5010105-09手動螢幕870630
5010105-21單槍投影機911125
5010105-34防潮箱870630
5010105-34防潮箱890629
5010301-01A電腦桌861028
5010301-01A電腦桌861028
5010301-01A電腦桌861028
5010301-01A電腦桌861028
5010301-01A電腦桌861028
5010301-01A辦公桌890421
5010301-01A木紋桌891031
5010302-01資訊學習中心服務櫃檯991022
5010302-11窗簾980215
5010302-11窗簾980215
5010302-11窗簾980215
5010302-11窗簾980215
5010302-11窗簾980215
5010303-01A鐵櫃890603
5010303-01A玻璃鐵櫃890603
5010303-01A三抽屜鐵櫃890603
5010303-01A機架櫃910820
5010307-23高架地板970827
5010307-23高架地板970827
5010307-23高架地板970827
5010307-23高架地板970827
5010307-23高架地板970827
5010307-23高架地板970827
2011年6月1日 星期三
A406
3030402-31施工遷移940815
3140101-03個人電腦940815
3140302-01網路雷射印表機900108
3140307-01顯示器940815
3140401-06還原卡940815
3140403-16集線器940815
3140503-001防火牆940815
3140503-001安裝設定費940815
3140506-001網路施工費940815
4050303-29教學廣播系統940815
5010102-09A白板880610
5010102-09A白板881202
5010106-03冷氣機971021
5010301-01A教師桌940815
5010302-02單面工作桌940815
5010302-02雙面工作桌940815
5010307-23高架地板970827
3140101-03個人電腦940815
3140302-01網路雷射印表機900108
3140307-01顯示器940815
3140401-06還原卡940815
3140403-16集線器940815
3140503-001防火牆940815
3140503-001安裝設定費940815
3140506-001網路施工費940815
4050303-29教學廣播系統940815
5010102-09A白板880610
5010102-09A白板881202
5010106-03冷氣機971021
5010301-01A教師桌940815
5010302-02單面工作桌940815
5010302-02雙面工作桌940815
5010307-23高架地板970827
A405
3140302-01雷射印表機931129
3140302-01印表機961130
3140302-04投幣式印表機網路控管器961130
3140304-06掃瞄器961130
3140401-01網路系統施工931130
3140403-16集線器931130
3140403-16集線器931130
3140503-001施工費961130
4050205-10監控設備961130
4050303-29教學廣播系統931130
5010102-09A白板881202
5010105-09手動螢幕870630
5010106-03冷氣機971021
5010301-01A電腦桌931130
5010302-11窗簾980215
5010307-23高架地板970827
63140503-01燒錄器961130
3140302-01印表機961130
3140302-04投幣式印表機網路控管器961130
3140304-06掃瞄器961130
3140401-01網路系統施工931130
3140403-16集線器931130
3140403-16集線器931130
3140503-001施工費961130
4050205-10監控設備961130
4050303-29教學廣播系統931130
5010102-09A白板881202
5010105-09手動螢幕870630
5010106-03冷氣機971021
5010301-01A電腦桌931130
5010302-11窗簾980215
5010307-23高架地板970827
63140503-01燒錄器961130
2010年3月27日 星期六
4-7 EXCEL與機率
4-7 EXCEL與機率
EXCEL提供了很多常用的機率函數,只要按【插入/函數】,在視窗"插入函數"內,從函數類別下選擇"統計",使可找到所要的機率函數。
一般機率的使用,常會出現兩個需求方向,以考試為例,如果考試完畢,知道?=48,?=13,則某一考生成績如果為68,其表現如何?再者如果想淘汰80%的考生,則及格標準應該定為多少?因此EXCEL在設計機率分配函數,通常給予機率分配函數及反分配函數。
4-7-1二項分配函數
傳回特定次數之二項分配機率值。使用BINOMDIST函數主要用於解決特定次數實驗的問題,每次實驗的結果不是成功就是失敗,且每次實驗皆為獨立,同時實驗成功的機率為一常數。
語法:
BINOMDIST(number_s,trials,probability_s,cumulative)
Number_s:欲求解的實驗成功次數。
Trals:獨立實驗的次數
Probability_s:每一次實驗的成功機率。
Cumulative:為一邏輯值,主要用來決定函數的型態。如果cumulative為TRUE,則傳回累加分配函數值,其代表最多number_s次成功的機率;如果其值為FALSE,則傳回機率密度函數的機率值,代表有number_s次成功的機率。
例題34:
擲一枚銅板出現正面的機率為0.5,則在10次實驗中恰出現6次正面的機率為:
解:BINOMDIST(6,10,0.5,FALES)等於0.205078
例題35:
在某一地區中,5個70歲的老人中,有3個可以活到80歲。今從該地區中,隨機抽取10人,是求至少有8人,可以再多活10年的機率?
解:P(至少有8人)=1-P(至多有7人)
=1-BINOMDIST(7,10,0.6,TRUE)
=1-0.83271=0.16729
4-7-2卜瓦松分配函數
傳回卜瓦松機率分配。卜瓦松分配常見的應用,係在於預測特定時間內事件發生的次數,例如,在一分鐘內到達收費站的汽車數。
語法:
POISSON(x,mean,cumulative)
X:是事件的次數
Mean:是期望值
Cumulative:是一個邏輯值,用來決定機率分配傳回值的格式。如果cumulative是TRUE,將傳回事件發生從0到X的累積卜瓦松機率;如果cumulative是FALSE,將傳回事件的數目正好是X的卜瓦松機率密度函數值。
例題36:
假設再高速公路上平均每天有五次車禍發生,若X為某一天發生車禍之隨機變數,求下列各項機率:
(1)沒有發生車禍。
(2)至多2次車禍
解:(1)P(X=0)=POISSON(0,5,FALSE)=0.006737947
(2)P(X≦2)=POISSON(2,5,TRUE)=0.124652019
4-7-3常態分配函數
根據指定之平均數和標準差,傳回其常態累積分配函數。本函數廣泛應用於包括假設檢定統計學之應用。
語法:
NORMDIST(x,mean,standard_dev,cumulative)
X:是要求分配之數值。
Mean:是此分配的算術平均數。
Stand_dev:是分配的標準差。
Cumulative:是決定函數形式的邏輯值。如果Cumulative是TRUE,則傳回累積分配函形式的邏輯值。如果是FALSE,則傳回機率密度函數值。
例題37:
以考試為例,如果考試完畢,知道?=48,?=13,則某一考生成績為68,其表現如何?
解:
P(小於等於68)=NORMDIST(68,48,13,TRUE)等於0.938032081。
考試成績比該考生差的人約有93.8%。
4-7-4常態分配函數之反函數
根據指定的平均數和標準差,傳回其常態累積分配函數之反函數。
語法:
NORMINV(probability,mean,standard_dev)
Probability:是符合常態分配的機率。
Mean:是此分配的算術平均數。
Standard_dev:是此分配的標準差。
例題38:
以考試為例,如果考試完畢,知道?=48,?=13,如果想淘汰80%的考生,則及格標準應該定為多少?
解:NORMINV(0.80,48,13)等於58.94107802,及格標準應該定為59分。
4-7-5標準常態分配函數
傳回標準常態累積分配函數。此分配的平均值是0和標準差1。利用此含數可代替標準常態分配函數曲線之表格。
語法:
NORMSDUST(z)
Z:是要分配的數值。
例題39:
P(標準常態分配≦1.96)
解:NORMSDIST(1.96)等於0.975002175
例題40:
假設成人男性體重接近常態分布,其平均值?=65公斤,標準差?=7公斤,則成人男性體重介於60公斤與70公斤者之機率為多少?
解:
P(60≦X≦70)=P〔(60-62)/7≦(X-62)/7≦(70-62)/7〕
=P(-0.2857≦Z≦1.1429)
=NORMSDIST(1.1429)-NORMSDIST(-0.2857)
=0.873459892-0.387554015=0.485905877
4-7-6標準常態分配函數之反函數
傳回平均數為0且標準差為1的標常態累積分配函數的反函數。
語法:
NORMISNV(probability)
Probability:是對應於常態分配的機率。
例題41:
若P(標準常態分配≦z)=0.90,則z=?
解:z=NORMSINV(0.90)=1.281550794
4-7-7 t分配函數
傳回Student氏之t分配。t分配適用於小樣本資料組的假設檢定。使用此函數就不用建一個t分配的臨界值表格。
語法:
TDIST(x,degrees_freedom,tails)
X:是要用來評估分配的數值。
Degrees_freedom:是用來指出自由度的整數。
Tails:指定要傳回的分配尾數得個數。如果tails=1,則TDIST傳回單尾分配。如果tails=2,則TDIST傳雙尾分配。
例題42:
若自由度25,P(T≧2)=TDIST(2,25,1)=0.028237989。
若自由度為60,P(∣T∣≧1.96)=TDIST(1.96,60,2)
=0.054644927。
4-7-8 t分配函數值之反函數
傳回只贈自由度的Student氏的反t分配。
語法:
TINV(probability,degrees_freedom)
Probability:是一個雙尾Student氏t-分配的機率值。
Degrees_freedom:是構成該分配的自由度數目。
例題43:
若自由度為60,P(∣T∣≧t)=0.054645,則t=?
解:t=TINV(0.054645,60)=1.96
4-7-9卡方分配函數
傳回單尾卡分配的機率值。?分配與?測試有關。?是用來比較觀測值和預期值的差異。例如就遺傳學的經驗,假設植物會繼承上一代的特定顏色。藉由比較觀察結果和原先的預測,您可以決定原先的假設是否有效。
語法:
CHIDIST(x,degrees_freedom)
x:為用以進行?檢定的數值。
degrees_freedom:及自由度。
例題44:
若自由度為10,P(X>18.307)=?
解:P(X>18.307)=CHIDIST(18.307,10)=0.050001
4-7-10卡方分配函數之反函數
傳回單尾卡方分配的反函數值。
語法:
CHINV(probability,degrees_freedom)
Probability:為卡方分配所使用的機率。
Degrees_freedom:為自由度。
例題45:
若自由度為10,P(X>a)=0.05,求a=?
解:a=CHINV(0.05,10)=18.30703
4-7-11 F分配函數
傳回F機率分配。您可以使用這項函數來決定兩組資料是否有不同的變異程度。例如,您可以檢查男生和女生高中入學成績,是否女生成績的變異程度不同於男生。
語法:
FDIST(x,degrees_freedom1,degreed_freedom2)
X:為用來求算此函數的參數數值。
Degrees_freedom1:為分子的自由度。
Degrees_freedom2:為分母的自由度。
例題46:
是求分子自由度為6,分母自由度為4,P(F>15.20675)=?
解:P(F>15.20675)=FDIST(15.20675,6,4)=0.01
4-7-12 F分配函數之反函數
傳回F機率分配的反函數值。如果p=FDIST(x,…),則FINV(p,…)=?F機率分配苦子在F檢定中使用,F檢定是用來比較兩組資料的變異程度。例如,您可以分析美國和加拿大的收入分配,以找出這兩個國家收入的變異程度是否相似。
語法:
FINV(probability,degrees_freedom1,degrees_freedom2)
Probability:是和F累加分配有關的機率值。
Degrees_ freedom1:為分子的自由度。
Degrees_freedom2:為分母的自由度。
例題47:
是求自由度為5、10,P(F≦a)=0.95之臨界值a。
解:若P(F≦a)=0.05。
a=FINV(0.05,5,10)=3.325837
EXCEL提供了很多常用的機率函數,只要按【插入/函數】,在視窗"插入函數"內,從函數類別下選擇"統計",使可找到所要的機率函數。
一般機率的使用,常會出現兩個需求方向,以考試為例,如果考試完畢,知道?=48,?=13,則某一考生成績如果為68,其表現如何?再者如果想淘汰80%的考生,則及格標準應該定為多少?因此EXCEL在設計機率分配函數,通常給予機率分配函數及反分配函數。
4-7-1二項分配函數
傳回特定次數之二項分配機率值。使用BINOMDIST函數主要用於解決特定次數實驗的問題,每次實驗的結果不是成功就是失敗,且每次實驗皆為獨立,同時實驗成功的機率為一常數。
語法:
BINOMDIST(number_s,trials,probability_s,cumulative)
Number_s:欲求解的實驗成功次數。
Trals:獨立實驗的次數
Probability_s:每一次實驗的成功機率。
Cumulative:為一邏輯值,主要用來決定函數的型態。如果cumulative為TRUE,則傳回累加分配函數值,其代表最多number_s次成功的機率;如果其值為FALSE,則傳回機率密度函數的機率值,代表有number_s次成功的機率。
例題34:
擲一枚銅板出現正面的機率為0.5,則在10次實驗中恰出現6次正面的機率為:
解:BINOMDIST(6,10,0.5,FALES)等於0.205078
例題35:
在某一地區中,5個70歲的老人中,有3個可以活到80歲。今從該地區中,隨機抽取10人,是求至少有8人,可以再多活10年的機率?
解:P(至少有8人)=1-P(至多有7人)
=1-BINOMDIST(7,10,0.6,TRUE)
=1-0.83271=0.16729
4-7-2卜瓦松分配函數
傳回卜瓦松機率分配。卜瓦松分配常見的應用,係在於預測特定時間內事件發生的次數,例如,在一分鐘內到達收費站的汽車數。
語法:
POISSON(x,mean,cumulative)
X:是事件的次數
Mean:是期望值
Cumulative:是一個邏輯值,用來決定機率分配傳回值的格式。如果cumulative是TRUE,將傳回事件發生從0到X的累積卜瓦松機率;如果cumulative是FALSE,將傳回事件的數目正好是X的卜瓦松機率密度函數值。
例題36:
假設再高速公路上平均每天有五次車禍發生,若X為某一天發生車禍之隨機變數,求下列各項機率:
(1)沒有發生車禍。
(2)至多2次車禍
解:(1)P(X=0)=POISSON(0,5,FALSE)=0.006737947
(2)P(X≦2)=POISSON(2,5,TRUE)=0.124652019
4-7-3常態分配函數
根據指定之平均數和標準差,傳回其常態累積分配函數。本函數廣泛應用於包括假設檢定統計學之應用。
語法:
NORMDIST(x,mean,standard_dev,cumulative)
X:是要求分配之數值。
Mean:是此分配的算術平均數。
Stand_dev:是分配的標準差。
Cumulative:是決定函數形式的邏輯值。如果Cumulative是TRUE,則傳回累積分配函形式的邏輯值。如果是FALSE,則傳回機率密度函數值。
例題37:
以考試為例,如果考試完畢,知道?=48,?=13,則某一考生成績為68,其表現如何?
解:
P(小於等於68)=NORMDIST(68,48,13,TRUE)等於0.938032081。
考試成績比該考生差的人約有93.8%。
4-7-4常態分配函數之反函數
根據指定的平均數和標準差,傳回其常態累積分配函數之反函數。
語法:
NORMINV(probability,mean,standard_dev)
Probability:是符合常態分配的機率。
Mean:是此分配的算術平均數。
Standard_dev:是此分配的標準差。
例題38:
以考試為例,如果考試完畢,知道?=48,?=13,如果想淘汰80%的考生,則及格標準應該定為多少?
解:NORMINV(0.80,48,13)等於58.94107802,及格標準應該定為59分。
4-7-5標準常態分配函數
傳回標準常態累積分配函數。此分配的平均值是0和標準差1。利用此含數可代替標準常態分配函數曲線之表格。
語法:
NORMSDUST(z)
Z:是要分配的數值。
例題39:
P(標準常態分配≦1.96)
解:NORMSDIST(1.96)等於0.975002175
例題40:
假設成人男性體重接近常態分布,其平均值?=65公斤,標準差?=7公斤,則成人男性體重介於60公斤與70公斤者之機率為多少?
解:
P(60≦X≦70)=P〔(60-62)/7≦(X-62)/7≦(70-62)/7〕
=P(-0.2857≦Z≦1.1429)
=NORMSDIST(1.1429)-NORMSDIST(-0.2857)
=0.873459892-0.387554015=0.485905877
4-7-6標準常態分配函數之反函數
傳回平均數為0且標準差為1的標常態累積分配函數的反函數。
語法:
NORMISNV(probability)
Probability:是對應於常態分配的機率。
例題41:
若P(標準常態分配≦z)=0.90,則z=?
解:z=NORMSINV(0.90)=1.281550794
4-7-7 t分配函數
傳回Student氏之t分配。t分配適用於小樣本資料組的假設檢定。使用此函數就不用建一個t分配的臨界值表格。
語法:
TDIST(x,degrees_freedom,tails)
X:是要用來評估分配的數值。
Degrees_freedom:是用來指出自由度的整數。
Tails:指定要傳回的分配尾數得個數。如果tails=1,則TDIST傳回單尾分配。如果tails=2,則TDIST傳雙尾分配。
例題42:
若自由度25,P(T≧2)=TDIST(2,25,1)=0.028237989。
若自由度為60,P(∣T∣≧1.96)=TDIST(1.96,60,2)
=0.054644927。
4-7-8 t分配函數值之反函數
傳回只贈自由度的Student氏的反t分配。
語法:
TINV(probability,degrees_freedom)
Probability:是一個雙尾Student氏t-分配的機率值。
Degrees_freedom:是構成該分配的自由度數目。
例題43:
若自由度為60,P(∣T∣≧t)=0.054645,則t=?
解:t=TINV(0.054645,60)=1.96
4-7-9卡方分配函數
傳回單尾卡分配的機率值。?分配與?測試有關。?是用來比較觀測值和預期值的差異。例如就遺傳學的經驗,假設植物會繼承上一代的特定顏色。藉由比較觀察結果和原先的預測,您可以決定原先的假設是否有效。
語法:
CHIDIST(x,degrees_freedom)
x:為用以進行?檢定的數值。
degrees_freedom:及自由度。
例題44:
若自由度為10,P(X>18.307)=?
解:P(X>18.307)=CHIDIST(18.307,10)=0.050001
4-7-10卡方分配函數之反函數
傳回單尾卡方分配的反函數值。
語法:
CHINV(probability,degrees_freedom)
Probability:為卡方分配所使用的機率。
Degrees_freedom:為自由度。
例題45:
若自由度為10,P(X>a)=0.05,求a=?
解:a=CHINV(0.05,10)=18.30703
4-7-11 F分配函數
傳回F機率分配。您可以使用這項函數來決定兩組資料是否有不同的變異程度。例如,您可以檢查男生和女生高中入學成績,是否女生成績的變異程度不同於男生。
語法:
FDIST(x,degrees_freedom1,degreed_freedom2)
X:為用來求算此函數的參數數值。
Degrees_freedom1:為分子的自由度。
Degrees_freedom2:為分母的自由度。
例題46:
是求分子自由度為6,分母自由度為4,P(F>15.20675)=?
解:P(F>15.20675)=FDIST(15.20675,6,4)=0.01
4-7-12 F分配函數之反函數
傳回F機率分配的反函數值。如果p=FDIST(x,…),則FINV(p,…)=?F機率分配苦子在F檢定中使用,F檢定是用來比較兩組資料的變異程度。例如,您可以分析美國和加拿大的收入分配,以找出這兩個國家收入的變異程度是否相似。
語法:
FINV(probability,degrees_freedom1,degrees_freedom2)
Probability:是和F累加分配有關的機率值。
Degrees_ freedom1:為分子的自由度。
Degrees_freedom2:為分母的自由度。
例題47:
是求自由度為5、10,P(F≦a)=0.95之臨界值a。
解:若P(F≦a)=0.05。
a=FINV(0.05,5,10)=3.325837
2010年3月24日 星期三
PowerPoint必備快速鍵
PowerPoint必備快速鍵
上台簡報不但是現代大學生的必備基本功,更是大多數上班族每週都會碰到的例行公事,而製作一份簡報不但要發想內容,更要安排體結構和組織,要是這時遇到電腦跟你作對,處理不順遂,那可是氣死人了!其實在製作或是播放你的投影簡報檔案時,有許多鍵盤指令可以應用,不但可以編輯更快速、也可以在簡報時更輕鬆,就讓我們幫你選其中幾組快速鍵,看看怎麼增進你的效率!
快速鍵NO.1:
簡報翻頁免滑鼠,上下頁任你選!
說明簡報時大家都是使用滑鼠點一下進入下一頁,或是使用空白鍵換頁,只是有時按的太快,不小心切換到下一頁,卻看到簡報者使用滑鼠的右鍵選單來選取「前一頁」,其實用鍵盤簡單切換不是更方便?
切頁切過頭還再使用「前一頁」?
使用「上頁」、「下頁」來切換不但直覺而且簡便。
改用鍵盤切換以免選單出現破壞美觀畫面。
快速鍵NO.2:
標記註解更簡單,滑鼠筆跡馬上畫!
播放簡報的時候,常會需要配合解說指點畫面上的元件,不過通常都是自備一個雷射筆或是事先使用特效,其實PowerPoint裡頭有滑鼠軌跡的畫筆,不但明顯而且可以用鍵盤快速啟動喔!
簡報時畫面上有需要指點的東西,可以按下快速鍵開始標記。
馬上可以標記你想要的東西,也可以按下E來清除畫面上的標記。
最後可以按下離開標記模式。
快速鍵NO.3:
回顧章節,切換不用單頁翻動!
簡報結束後,常會有底下的聽眾發問,有時需要回顧章節,卻要一頁一頁的翻動,真是太過麻煩,要使用滑鼠右鍵的功能表,卻又顯的不美觀,其實投影片放映時,可以用快速鍵叫出內建的投影標題清單,讓你快速切換!
投影片好多張,但是卻要跳到某個章節,難道只能一頁頁切回去嗎?
按下快速鍵可以叫出所有的投影片標題列表。只要利用滑鼠輕點或是鍵盤選取就可以簡單跳頁喔!
快速鍵NO.4:
物件移動對不準,格線讓你更輕鬆!
圖片、視訊、表格,做簡報的投影片總少不了各式各樣豐富的元件,適當的使用可以增添不少簡報的可看性,不過許多小小的圖片,對其排列總是那麼麻煩,還要滑鼠移半天才可以擺好,現在教你打開格線對齊它!
開了張圖片,想要好好地擺正,先按下快速鍵。
按下之後可以看到整齊的對齊用格線喔!
如此一來,擺正對齊就不是什麼難事了!
快速鍵NO.5:
學回組合鍵,標題層級隨你調整!
一份清楚明瞭的簡報,最重要的就是架構的安排,該下怎樣的標題才能切綱提領,該怎麼分項述說才能巨細靡遺,這些都是需要細細考量的,學會快速鍵讓你改變架構、標題的層級變的更簡單,更容易組織你的資訊!
按下組合建跟左鍵提升層級右鍵降低層級。
標題下了才發現架構不對,想要在分項。
這樣調整架構更方便,組織更清楚!
鍵NO.6:
按下快速鍵!新增投影片更簡單!
作投影片不可能只有兩三張吧?不過要怎麼新增投影片?你或許會說:「進『插入』選單選擇『插入新投影片』啊」,其實還有更快的方法喔!只要簡單按下快速鍵,新的投影片就會自動插入了!
要是不會使用快速鍵,就只能用傳統的選單方式加入新投影片。
但是這個動作也可以用這組快速鍵代替哦!
簡單就插入新投影片,是不是更有效率呢?
快速鍵NO.7:
單鍵切換更容易,不再點錯網址!
簡報的內容或多或少都會加入一些連結,有時連結是網址,可以直接連上網路觀看想要陳述的網頁,有時連結是影片,會自動開啟電腦中的影片讓聆聽簡報的人觀賞,現在教你怎麼利用快速鍵在其中遨遊!
打開滿是連結的投影片,該怎麼用鍵盤選連結?
只要輕按幾下,就會在畫面上的連結中切換哦!
其實只要簡單一個按鍵,就可以循環選取。
上台簡報不但是現代大學生的必備基本功,更是大多數上班族每週都會碰到的例行公事,而製作一份簡報不但要發想內容,更要安排體結構和組織,要是這時遇到電腦跟你作對,處理不順遂,那可是氣死人了!其實在製作或是播放你的投影簡報檔案時,有許多鍵盤指令可以應用,不但可以編輯更快速、也可以在簡報時更輕鬆,就讓我們幫你選其中幾組快速鍵,看看怎麼增進你的效率!
快速鍵NO.1:
簡報翻頁免滑鼠,上下頁任你選!
說明簡報時大家都是使用滑鼠點一下進入下一頁,或是使用空白鍵換頁,只是有時按的太快,不小心切換到下一頁,卻看到簡報者使用滑鼠的右鍵選單來選取「前一頁」,其實用鍵盤簡單切換不是更方便?
切頁切過頭還再使用「前一頁」?
使用「上頁」、「下頁」來切換不但直覺而且簡便。
改用鍵盤切換以免選單出現破壞美觀畫面。
快速鍵NO.2:
標記註解更簡單,滑鼠筆跡馬上畫!
播放簡報的時候,常會需要配合解說指點畫面上的元件,不過通常都是自備一個雷射筆或是事先使用特效,其實PowerPoint裡頭有滑鼠軌跡的畫筆,不但明顯而且可以用鍵盤快速啟動喔!
簡報時畫面上有需要指點的東西,可以按下快速鍵開始標記。
馬上可以標記你想要的東西,也可以按下E來清除畫面上的標記。
最後可以按下
快速鍵NO.3:
回顧章節,切換不用單頁翻動!
簡報結束後,常會有底下的聽眾發問,有時需要回顧章節,卻要一頁一頁的翻動,真是太過麻煩,要使用滑鼠右鍵的功能表,卻又顯的不美觀,其實投影片放映時,可以用快速鍵叫出內建的投影標題清單,讓你快速切換!
投影片好多張,但是卻要跳到某個章節,難道只能一頁頁切回去嗎?
按下快速鍵可以叫出所有的投影片標題列表。只要利用滑鼠輕點或是鍵盤選取就可以簡單跳頁喔!
快速鍵NO.4:
物件移動對不準,格線讓你更輕鬆!
圖片、視訊、表格,做簡報的投影片總少不了各式各樣豐富的元件,適當的使用可以增添不少簡報的可看性,不過許多小小的圖片,對其排列總是那麼麻煩,還要滑鼠移半天才可以擺好,現在教你打開格線對齊它!
開了張圖片,想要好好地擺正,先按下快速鍵。
按下之後可以看到整齊的對齊用格線喔!
如此一來,擺正對齊就不是什麼難事了!
快速鍵NO.5:
學回組合鍵,標題層級隨你調整!
一份清楚明瞭的簡報,最重要的就是架構的安排,該下怎樣的標題才能切綱提領,該怎麼分項述說才能巨細靡遺,這些都是需要細細考量的,學會快速鍵讓你改變架構、標題的層級變的更簡單,更容易組織你的資訊!
按下組合建跟左鍵提升層級右鍵降低層級。
標題下了才發現架構不對,想要在分項。
這樣調整架構更方便,組織更清楚!
鍵NO.6:
按下快速鍵!新增投影片更簡單!
作投影片不可能只有兩三張吧?不過要怎麼新增投影片?你或許會說:「進『插入』選單選擇『插入新投影片』啊」,其實還有更快的方法喔!只要簡單按下快速鍵,新的投影片就會自動插入了!
要是不會使用快速鍵,就只能用傳統的選單方式加入新投影片。
但是這個動作也可以用這組快速鍵代替哦!
簡單就插入新投影片,是不是更有效率呢?
快速鍵NO.7:
單鍵切換更容易,不再點錯網址!
簡報的內容或多或少都會加入一些連結,有時連結是網址,可以直接連上網路觀看想要陳述的網頁,有時連結是影片,會自動開啟電腦中的影片讓聆聽簡報的人觀賞,現在教你怎麼利用快速鍵在其中遨遊!
打開滿是連結的投影片,該怎麼用鍵盤選連結?
只要輕按幾下,就會在畫面上的連結中切換哦!
其實只要簡單一個按鍵,就可以循環選取。
2010年3月19日 星期五
3-8 Excel 與敘述統計
3-8-1 由原始資料求敘述統計量
在這章所提到的平均數、中位數、眾數、變異數、標準差……,如果資料不多,直接用計算機倒也方邊,不過如果數據太多,任何人都會覺得很棘手,接下來我們以第二章的100個葉片長度數據為例,見識一下Excel的敘述統計。
步驟1
首先將原始資料輸入Excel儲存格範圍A1至A100中,為什麼不像第二章依樣,將資料輸入儲存格範圍A1至J10呢?這是因為Excel將不同欄位的資料視為不同組別的資料,如妥將資料範圍設成A1:J10後,執行EXCEL的敘述統計運算,則將得到10組的平均數、中位數、眾數、變異數、標準差……。
步驟2
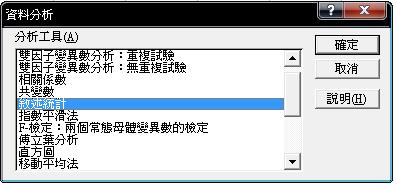
選取【工具/資料分析】,在分析工具下選【敘述統計】,按【確定】。
步驟3
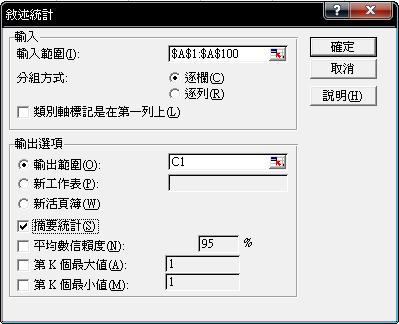
在敘述統計視窗下,鍵入
輸入範圍:A1:A100
分組方式:◎逐欄
輸出選項
輸出範圍:C1
□摘要統計
按【確定】。

3-8-2 由次數分配表求敘述統計量
雖然EXCEL沒友直接針對次數分配表,給予敘述統計功能的支援,但是利用自動填滿控制點的快速複製,重複上述步驟,也能迅速得到平均數、中位數、眾數、變異數、標準差……等。
◎ 步驟1:首先將原始資料輸入EXCEL儲存格範圍A1至C8。
◎ 步驟2:首先在儲存格D1,輸入147.5,將指標移到自動填滿控制點上,按住左鍵,向下拖曳到儲存格D2(因為第一組的組中點147.5有二位)
◎ 步驟3:在儲存格D3,輸入152.5,將指標移到自動填滿控制點上,按住左鍵,向下拖曳到儲存格D11(因為第二組的組中點152.5有9位)。
◎ 步驟4:重複上述步驟將資料輸入
◎ 步驟5:選取【工具/資料分析】,在分析工具下選【敘述統計】,按【確定】。
◎ 步驟6:在敘述統計視窗下,鍵入
輸入範圍:D1:D50
分組方式:逐欄
ˇ輸入選項
按【確定】。



3-8-3 EXCEL 與相關係數
例題19
請利用下表資料求出兩組數據的相關係數。
解:
步驟1:首先將原始資料輸入EXCEL儲存格範圍A1至F2
步驟2:選取【工具/資料分析】,在分析工具下選【相關係數】,按【確定】。
步驟3:在相關係數視窗下,鍵入
輸入範圍:A1:F2
分組方式:◎逐列
類別軸標記在第一欄上
新工作表
按【確定】。
由表中可知氮肥用量及稻穀產量的相關係數r=0.99822956。



在這章所提到的平均數、中位數、眾數、變異數、標準差……,如果資料不多,直接用計算機倒也方邊,不過如果數據太多,任何人都會覺得很棘手,接下來我們以第二章的100個葉片長度數據為例,見識一下Excel的敘述統計。
步驟1
首先將原始資料輸入Excel儲存格範圍A1至A100中,為什麼不像第二章依樣,將資料輸入儲存格範圍A1至J10呢?這是因為Excel將不同欄位的資料視為不同組別的資料,如妥將資料範圍設成A1:J10後,執行EXCEL的敘述統計運算,則將得到10組的平均數、中位數、眾數、變異數、標準差……。
步驟2
選取【工具/資料分析】,在分析工具下選【敘述統計】,按【確定】。
步驟3
在敘述統計視窗下,鍵入
輸入範圍:A1:A100
分組方式:◎逐欄
輸出選項
輸出範圍:C1
□摘要統計
按【確定】。



3-8-2 由次數分配表求敘述統計量
雖然EXCEL沒友直接針對次數分配表,給予敘述統計功能的支援,但是利用自動填滿控制點的快速複製,重複上述步驟,也能迅速得到平均數、中位數、眾數、變異數、標準差……等。
◎ 步驟1:首先將原始資料輸入EXCEL儲存格範圍A1至C8。
◎ 步驟2:首先在儲存格D1,輸入147.5,將指標移到自動填滿控制點上,按住左鍵,向下拖曳到儲存格D2(因為第一組的組中點147.5有二位)
◎ 步驟3:在儲存格D3,輸入152.5,將指標移到自動填滿控制點上,按住左鍵,向下拖曳到儲存格D11(因為第二組的組中點152.5有9位)。
◎ 步驟4:重複上述步驟將資料輸入
◎ 步驟5:選取【工具/資料分析】,在分析工具下選【敘述統計】,按【確定】。
◎ 步驟6:在敘述統計視窗下,鍵入
輸入範圍:D1:D50
分組方式:逐欄
ˇ輸入選項
按【確定】。



3-8-3 EXCEL 與相關係數
例題19
請利用下表資料求出兩組數據的相關係數。
解:
步驟1:首先將原始資料輸入EXCEL儲存格範圍A1至F2
步驟2:選取【工具/資料分析】,在分析工具下選【相關係數】,按【確定】。
步驟3:在相關係數視窗下,鍵入
輸入範圍:A1:F2
分組方式:◎逐列
類別軸標記在第一欄上
新工作表
按【確定】。
由表中可知氮肥用量及稻穀產量的相關係數r=0.99822956。



2010年3月17日 星期三
A404
2-05-3140101-03-407(A404)
個人電腦950414
3-04-3140302-01-53(A404)
雷射印表機950414
4-02-3140307-01-188(A404)
液晶螢幕950414
5-07-3140401-06-179(A404)
還原卡950414
5-14-3140403-30(A404)
交換式集線器950414
6-12-4050303-29-5(A404)
教學廣播系統950414
8-07-5010106-03-424(A404)
冷氣機971021
9-03-5010301-01A-2611(A404)
電腦鋼桌+LCD防盜固定座950414
28張
9-04-5010301-01A-2639(A404)
定型鋼桌+LCD固定座950414
教師
個人電腦950414
3-04-3140302-01-53(A404)
雷射印表機950414
4-02-3140307-01-188(A404)
液晶螢幕950414
5-07-3140401-06-179(A404)
還原卡950414
5-14-3140403-30(A404)
交換式集線器950414
6-12-4050303-29-5(A404)
教學廣播系統950414
8-07-5010106-03-424(A404)
冷氣機971021
9-03-5010301-01A-2611(A404)
電腦鋼桌+LCD防盜固定座950414
28張
9-04-5010301-01A-2639(A404)
定型鋼桌+LCD固定座950414
教師
訂閱:
意見 (Atom)